3.1: Introduction to statistical mechanics

Statistical mechanics is a branch of physical chemistry that acts as a bridge between quantum mechanics and classical mechanics. In quantum mechanics, particles are small, their states are quantized, and sample sizes are relatively small, whereas in classical mechanics particles are macroscopic, states are continuous, and sample sizes are on the order of Avogadro’s number (~10²³). A basic understanding of statistical mechanics can help us explain why chemical processes occur.

Consider a system that consists of an ideal gas at equilibrium. Imagine taking a 'snapshot' of that system that shows the location and energy of each particle in that instant. This is one possible microstate for the system in its given state. If we waited a few moments and took another 'snapshot', the individual locations of the particles and the distribution of energy between them would differ slightly, but the macroscopic state (temperature, pressure, volume etc.) of the system would still be the same. That is, this is a different microstate (a specific distribution of particles and energy) that results in the same overall state (also called a macrostate).

Some thermodynamic states have more microstates associated with them than others. Since all microstates (with a fixed energy) are equally probable, a thermodynamic state that can be achieved via more microstates is more probable than one associated with fewer microstates. Let's apply this concept to help understand diffusion.

Consider the box below with a divider (dotted line) in the middle that has two identical gas particle (labelled as red and blue to keep track of them) on the left side. Imagine that we remove the divider for a minute so that the particles can travel between the two sides of the box, then replace it back in the middle of the box. There are four equally likely final positions of the gas particles: (1) the red and blue particle could both be on the left, (2) the red and blue particle could both be on the right, (3) the blue particle could be on the left and the red on the right, or (4) the red particle could be on the left and the blue on the right. Each of these possibilities represents a different microstate.

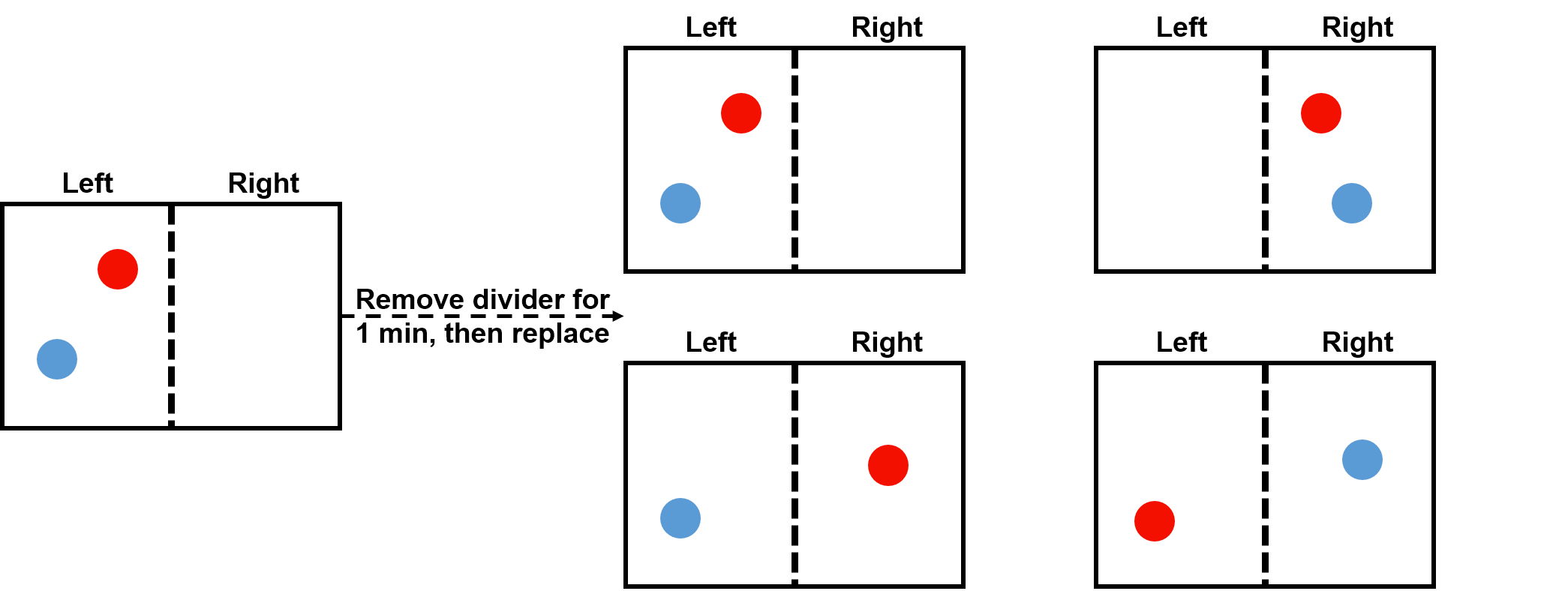
Since our particles are identical (recall the red and blue colours were just to help us keep track in the diagram), when observing the four possible outcomes it would not be possible to distinguish outcome (3) from outcome (4), since both result in one particle on each side. It would, however, be possible to observe whether there were two particles on the left, (1), versus two particles on the right, (2). That is, these four different possibilities represent three distinct overall outcomes (macrostates): (A) both particles remain on the left side (as in outcome 1), (B) both particles move to the right side (as in outcome 2), or (C) one particle remains on the left while the other has moved to the right (as in outcomes 3 and 4). Since there are two ways (microstates) to achieve this 3rd outcome, it is the most likely overall outcome (macrostate). That is, the gas particles diffuse (spread out) because this leads to the most probable state.

This concept of systems tending towards the most probable state is described by a state variable, entropy (S), which is defined as

where k_B=1.38 x 10^-23 J/K is the Boltzmann constant and W is the number of microstates associated with our thermodynamic state of interest. Notice that a thermodynamic state has higher entropy (S) when it is associated with more microstates (W). That is, entropy is associated with a thermodynamic state's probability: more probable states have higher entropy.

We can use this statistical mechanical interpretation of entropy to intuitively predict entropy changes. Entropy will generally increase when there are more ways to distribute the positions and energies of particles (more microstates). Thus, entropy tends to increase when

• volume increases
• phase changes in the direction solid → liquid → gas
• a solid dissolves
• the number of moles of gas increases
• the temperature increases (associated with an increase in energy)
• the complexity of the molecular structure increases (more complex structures have more ways to distribute energy through vibrations and rotations)

Interactive: