3.3: Molecular Orbital (MO) Theory

Valence Bond theory is very useful and provides a fairly accurate and versatile framework to understand both reactivity and molecular geometry. However, electronic transitions between orbitals are very poorly predicted. Many of these problems are due to two key simplifications: (1) only valence electrons need to be considered during bonding and (2) the theory of hybridization. In reality, both simplifications are incorrect and manifest themselves in select circumstances.

The most accurate theory of bonding is Molecular Orbital (MO) theory. Two key differentiating aspects of MO theory compared to the other bonding theories that we have discussed are (1) in MO theory, electrons are not constrained to bonds but are rather spread throughout the whole molecule in molecular orbitals, as opposed to atomic orbitals, and (2) all electrons are considered.

The key aspect of MO theory is the construction of molecular orbitals through the combination of atomic orbitals. Schematically, we can represent this construction of MOs in a MO diagram. To construct these MO diagrams, we are going to first treat each atom independently, and then analyze the bonding interactions of the orbitals when they are brought in close proximity to each other. For example, in the simplest case H₂, the atomic orbitals of each hydrogen atoms are included in the left and right sides of the diagram. As the orbitals are brought closer together (indicated by the dotted lines), there is both a bonding interaction (leading to a σ-orbital, the bonding orbital), and a corresponding antibonding interaction (leading to a σ*-orbital, the antibonding orbital). Conceptually, this is similar to constructive and destructive wave interference.

The bond order can be determined by:

In the case of hydrogen, there are two electrons in the bonding orbital and none in the antibonding orbital. Therefore, the bond order is 1, which is consistent with the Valence Bond analysis that shows a single bond between the two hydrogens. For H₂, the highest occupied molecular orbitals (HOMO) is the σ-orbital and the lowest unoccupied molecular orbital (LUMO) is the σ*-orbital.

Lets do a similar analysis for He₂. While the diagram is similar to H₂, each He atom has an extra electron in the atomic orbital, which leads to a completely filled antibonding orbital. The bond order of He₂ is 0, which predicts that no bond should be formed between the two atoms. This explains why He₂ is impossible to form.

Lets now go to a more complicated diatomic, O₂. As you can see, the complexity of the diagram increases considerably. Not only are the 1s and 2s interactions included, but the 2p interactions provide both σ- and π-bonding orbitals as well as σ*- and π*-antibonding orbitals.

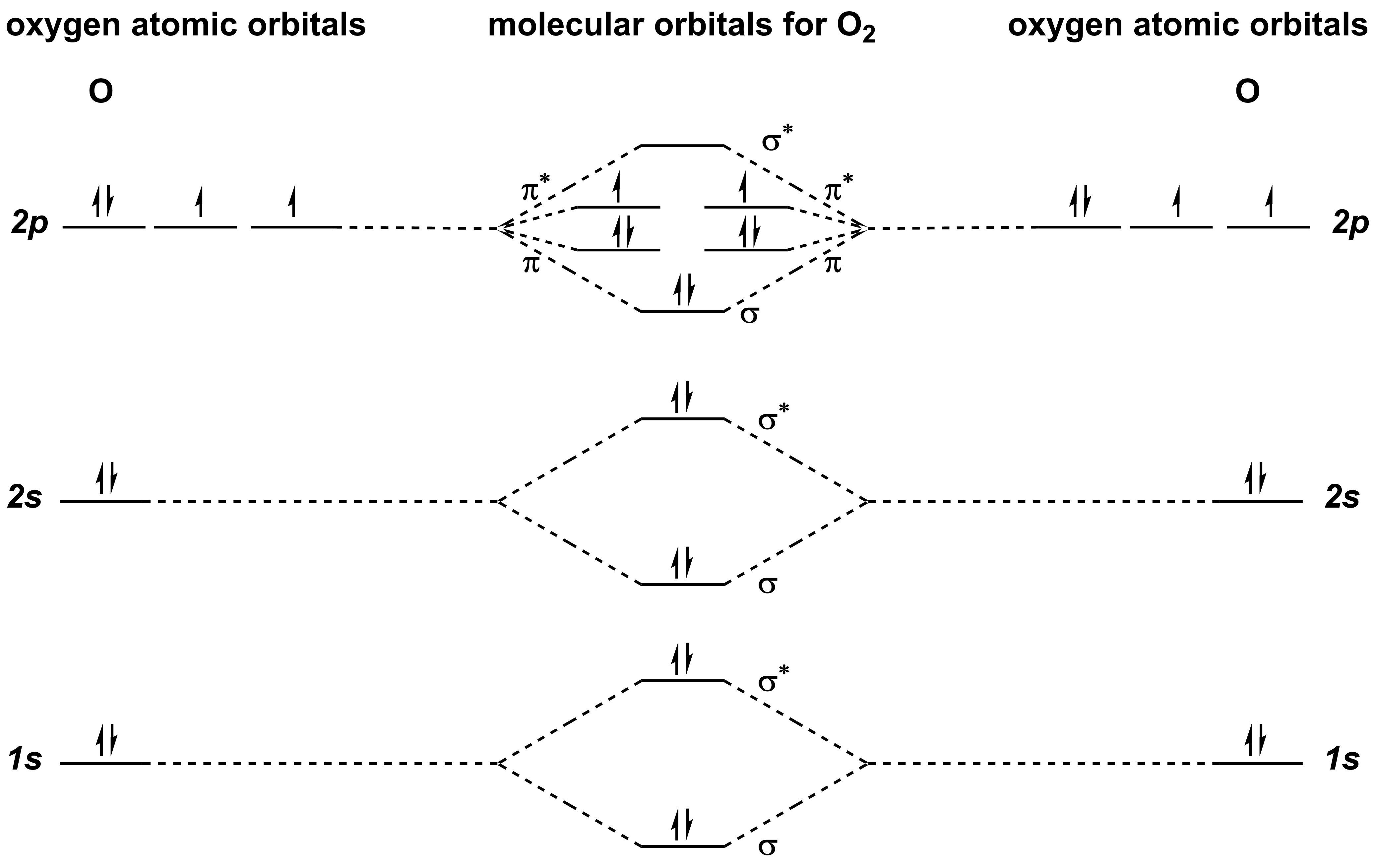
According to this diagram, you would predict that O₂ has a bond order of 2 (bond order = bonding electrons-antibonding electrons) and is paramagnetic (has unpaired electrons). However, this is not in agreement with Valence Bond theory. if you analyze O₂ using Valence Bond theory, you would predict that O₂ also has a bond order of 2 (i.e. double bond), but is diamagnetic (does not have unpaired electrons). Analysis of molecular oxygen reveals that it is, in fact, paramagnetic and MO theory provides the more accurate prediction.

Organic chemists do not frequently use pure MO theory. If MO theory is more quantitative and uses fewer assumptions than Valence Bond theory, why is it not used more frequently? The answer lies in the complexity of the diagrams and the difficulty to rapidly construct them for larger molecules. All the examples we have provided so far are simple diatomics. However, when the molecules get larger, the diagrams become increasingly more difficult to construct rapidly. For example, the MO diagram of a simple molecule such as ammonia is non-trivial (note, construction of this MO diagram is outside the scope of this course).

Similarly, the MO diagram for another small molecule, BF₃, is also not simple.

Instead of relying on the complex MO diagrams for larger organic molecules, organic chemists rely on a simplification of MO Theory called Frontier Molecular Orbital Theory. Frontier Molecular Orbital Theory focuses only on the interactions of the HOMO and LUMO, which creates a much simpler MO diagram that can still explain reactivity. Frontier Molecular Orbital Theory is described in the next section (3.4).

MO diagrams were covered and examined in detail in CHEM 111/121. A review of MO diagrams is included here, since we will apply some of these concepts later in the course. This section is included to provide theoretical background that we will build on later. No practice is included here because you will not be asked to produce MO diagrams of diatomic species like those shown above in this course.