1.6 Zeroth order integrated rate law

The integrated rate law for a zeroth order reaction is $[A]_t=-kt+[A]_0$ .

Consider if the reaction

$A\rightarrow B$ .

was found to have the experimental rate law

$rate=k[A]^0=k$ .

That is, the rate does not depend on the concentration of reaction A. This is called a zeroth order reaction. It might seem strange that a reaction’s rate doesn’t depend on how much of the reactant is present. However, consider if this reaction requires a catalyst such as an enzyme to happen. If there is a limited amount of enzyme and all of the enzymes are already being used (saturated), then adding more reactant A won’t change the rate of the reaction. This is an example of a zeroth order process.

We can determine how [A] changes over time, t, using the same method as in Part 2 Sections 1.4 and 1.5. Please read Section 1.4 before proceeding with the rest of this page, especially if you aren’t familiar with integral calculus.

For our zeroth order reaction, the differential rate law is

$-\frac{d[A]}{dt}=k$ .

Isolating the concentration terms on the left and the time terms on the right gives

$d[A]=-kdt$ .

Integrating the left side from the initial concentration, $[A]_0$ , to the concentration at time t, $[A]_t$ and the right side from time t=0 to t gives

$\int_{[A]_0}^{[A]_t}d[A]=\int_{0}^{t}-kdt$

$[A]\biggr\rvert_{[A]_{0}}^{[A]_{t}}=-kt\biggr\rvert_{0}^{t}$

$[A]_t-[A]_0=-kt$

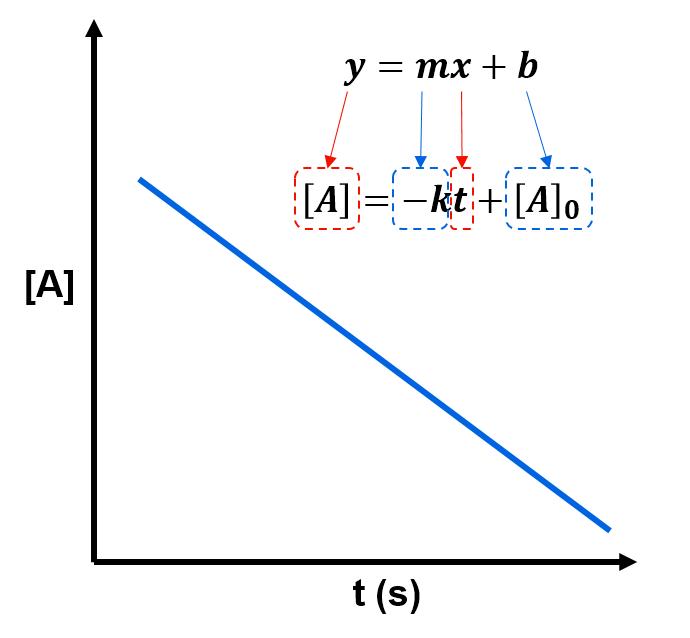
By rearranging this equation, as below,

$[A]_t=-kt+[A]_0$

we can see that a plot of $y=[A]_t$ vs $x=t$ should give a linear plot with slope $m=-k$ and y-intercept $b=[A]_0$ .

+ Practice

Interactive:

+ Feedback

Last updated on February 7, 2019 @9:36 am

1.6 Zeroth order integrated rate law

Search

Report