4.2: Standard Gibbs free energy

The change in standard Gibbs free energy, ΔG^o, for a reaction is the difference in free energy between the pure products at standard state and the pure reactants at standard state.
$\Delta G_{rxn}^{o}=\sum_{products} m\Delta G_{f}^{o}-\sum_{reactants} n\Delta G_{f}^{o}$
$\Delta G_{f}^{o}=0&space;kJ/mol$ for pure elements in their standard states.
The sign of $\Delta G$ indicates whether a reaction is spontaneous ( $\Delta G<0$ ) or non-spontaneous ( $\Delta G>0$ ) when given a specified proportion of reactants and/or products.
At equilibrium, the relationship between $\Delta G$ and $\Delta G^{o}$ is given by $\inline&space;\Delta G=\Delta G^{o}+RTlnQ=0$
$\Delta G^{o}$ defines the position of the equilibrium via $\inline&space;\Delta G^{o}=-RTlnK$

The change in standard Gibbs free energy, ΔG^o, for a reaction is the difference in free energy between the pure products at standard state and the pure reactants at standard state.

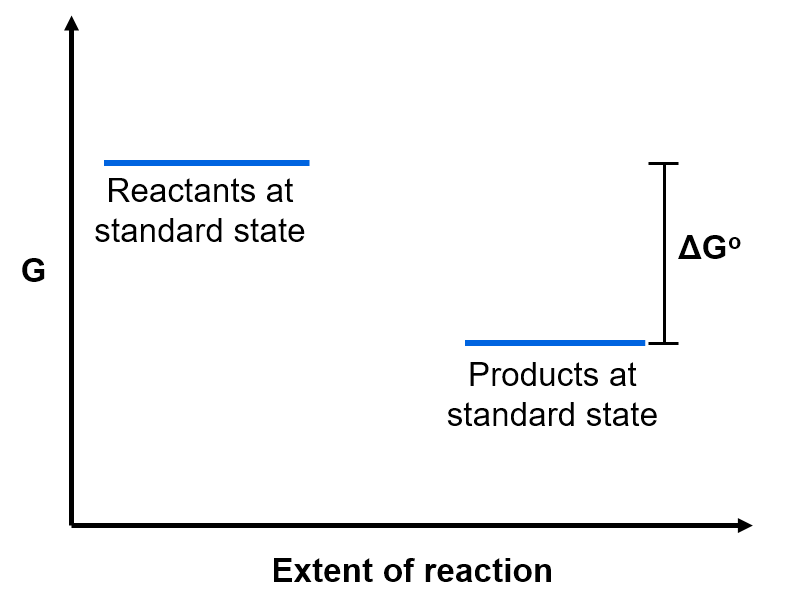
In the example above, $\Delta G^{o}<0$ because the Gibbs free energy of the products at standard state is lower than the Gibbs free energy of the reactants at standard state.

As with any state variable, we can use a variation of Hess' Law to calculate the change in standard Gibbs free energy using tabulated free energy of formation data. The free energy of formation is the free energy change associated with the formation of a molecule from its pure elements at standard state (see formation reactions). The standard Gibbs free energy change of the reaction is given by the difference between the free energy of formation for the products and reactants.

$\Delta G_{rxn}^{o}=\sum_{products} m\Delta G_{f}^{o}-\sum_{reactants} n\Delta G_{f}^{o}$

$\Delta G^{o}$ depends on $\Delta H^{o}$ via

$\Delta G^{o}=\Delta H^{o}-\Delta (TS^{o})$ .

Just as we set $\Delta H_{f}^{o}=0kJ/mol$ for pure elements in their standard states as a reference value, $\Delta G_{f}^{o}$ is also set to 0 kJ/mol for pure elements in their standard state as a reference point.

Example: Calculate $\Delta G_{rxn}^{o}$ for the reaction below, given that $\Delta G_{f}^{o}$ is -394.6 kJ/mol for CO₂, -228.4 kJ/mol for H₂O, and -50.8 kJ/mol for CH₄:

$CH_{4}+2O_{2}\rightarrow 2CO_{2}+2H_{2}O$

View solution:

$\Delta G_{rxn}^{o}=\sum_{products} m\Delta G_{f}^{o}-\sum_{reactants} n\Delta G_{f}^{o}$
$=[2(-228.4 kJ/mol)+2(-394.6)]-[1(-50.8 kJ/mol)+2(0 kJ/mol)]$
$=-1195 kJ/mol$

Note that each $\Delta G_{f}^{o}$ value is multiplied by the coefficient in the balanced reaction, and that $\Delta G_{f}^{o}$ is 0 kJ/mol for O₂.

$\Delta G^{o}$ tells us about the difference in free energy between reactants and products at standard state, but cannot predict the spontaneity of a reaction, since reactions don't occur under conditions of standard state. Instead, we rely on $\Delta G$ values to predict the spontaneity of a reaction. The value of $\Delta G$ reflects how far away any specified proportion of reactants and/or products is from the equilibrium position. The sign of $\Delta G$ reflects whether the reaction would have to proceed forward towards products ( $\Delta G<0$ ) or backwards towards reactants ( $\Delta G>0$ ) to reach equilibrium. The magnitude of $\Delta G$ reflects how far away the specified reaction position is from the equilibrium position. Reaction positions associated with smaller $\Delta G$ magnitudes are closer to equilibrium. Since a reaction gets closer and closer to equilibrium as it progresses, the magnitude of $\Delta G$ decreases as the reaction progresses. Once the reaction reaches equilibrium, $\Delta G=0$ . Note that $\Delta G^{o}$ does not change as the reaction progresses because the free energy difference between pure reactants and pure products at standard state does not change with reaction progress.

You can explore the relationships between the reaction extent (current position), equilibrium position, $\Delta G$ , and $\Delta G^{o}$ by dragging the slider below:

What is true of the current position (compared to equilibrium) when ΔG<0?

When ΔG<0, the ratio of reactants to products in the current position is higher than at equilibrium. That is, there are are more reactants (red dots) and fewer products (blue dots) than at equilibrium. This reaction will proceed spontaneously in the forward direction.

What is true of the current position (compared to equilibrium) when ΔG=0?

When ΔG=0, the ratio of reactants to products is the same in the current and equilibrium positions. That is, the reaction is at equilibrium.

What is true of the current position (compared to equilibrium) when ΔG>0?

When ΔG>0, the ratio of reactants to products in the current position is lower than at equilibrium. That is, there are are fewer reactants (red dots) and more products (blue dots) than at equilibrium. This reaction will proceed spontaneously in the reverse direction.

As illustrated in the above slider, the value of ΔG relates to the current position of the reaction (i.e. the relative number of reactants vs products). We can quantify the current position using the reaction quotient, Q. The reaction quotient, $Q$ , is defined similarly to the equilibrium constant, $K$ , in that it relates to the ratio of products over reactants. For example, $Q$ for the reaction

$aA+bB\rightarrow cC+dD$

is given by

$Q=\frac{[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}$ .

In the equation above, each concentration term reflects the current state of the system. Note that this is different than K, where the concentration terms must be equilibrium concentrations. K is the special name given to Q when a system is at equilibrium.

Review: Equilibrium

Chemical equilibrium is the state where reactants and products are both present and their concentrations do not change. Consider the reaction

$aA+bB\leftrightharpoons cC+dD$ .

At equilibrium, the forward reaction ( $aA+bB\rightarrow cC+dD$ ) proceeds at the same rate as the reverse reaction ( $cC+dD\rightarrow aA+bB$ ), such that there is no net change in the amount of A, B, C, or D.

The rates of the forward and reverse reactions are only equal when the relative proportions of the reactants and products satisfy the equilibrium constant, K, where K is defined as

$K=\frac{[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}$ (Equation 2)

and [A], [B], [C], and [D] are the concentrations of the reactants and products at equilibrium.

Removing reactants (A or B) from the reaction would immediately decrease the rate of the forward reaction while the rate of the reverse reaction remains unchanged. The relatively higher rate of the reverse reaction would result in a net increase of reactants (A and B) and a net decrease in products (C and D) until equation 2 is satisfied again. That is, the reaction would 'shift' towards the reactant side to counteract the removal of reactants. This tendency of an equilibrium reaction to counteract any change is referred to as le Chatelier's Principle. Similarly, removing products (C or D) would cause the reaction to 'shift' towards the product side to re-establish equilibrium.

The value of ΔG relates to the current position of the system, Q, by

$\Delta G=\Delta G^{o}+RTlnQ$ (Equation 1)

The derivation of Equation 1 is beyond the scope of this course. At equilibrium, ΔG=0 and Q=K, so we can rewrite this equation as

$0=\Delta G^{o}+RTlnK$ (Equation 2)

Rearranging Equation 2 above shows the relationship between $\Delta G^{o}$ and $K$ .

$\Delta G^{o}=-RTlnK$ (Equation 3).

That is, $\Delta G^{o}$ defines the position of the equilibrium. Note that while we used the condition of equilibrium to help us arrive at Equation 3, this equality is true even when the reaction is not at equilibrium, since $\Delta G^{o}$ has the same value no matter what position the reaction is in.

Example: What is the equilibrium constant, $K$ , for a reaction that has $\Delta G^{o}=-152&space;kJ/mol$ at 273 K?

View solution:

$\Delta G^{o}=-RTlnK$
$K=e^{\frac{-\Delta G^{o}}{RT}}$
$K=e^{\frac{-(-154000 \frac{J}{mol}}{(8.314 \frac{J}{mol K})(273 K)}}$
$K=1.21\times&space;10^{29}$

Note that $\Delta G^{o}=-152&space;kJ/mol$ was converted to $\Delta G^{o}=-152000&space;J/mol$ to cancel with the units of R.

We can understand the relationship between ΔG^o and K conceptually by recalling that G^o relates to $S_{univ}$ ( $\Delta G^o=-T\Delta S_{univ}$ at constant temperature and pressure) and thus to the probability associated with a state. States with lower G^o (higher $S_{univ}$ ) are associated with more probable states and states with higher G^o (lower $S_{univ}$ ) are associated with less probable states. At equilibrium we'd expect the relative amount of each chemical species to correspond to its Gibbs free energy: chemical species with lower G^o (higher $S_{univ}$ / probability) are present in greater amounts than chemical species with higher G^o (lower $S_{univ}$ / probability).

To visualize this relationship between $\Delta G^{o}$ and $K$ , consider the simple reaction

$A\rightarrow B$

with three different values of $\Delta G^o$ .

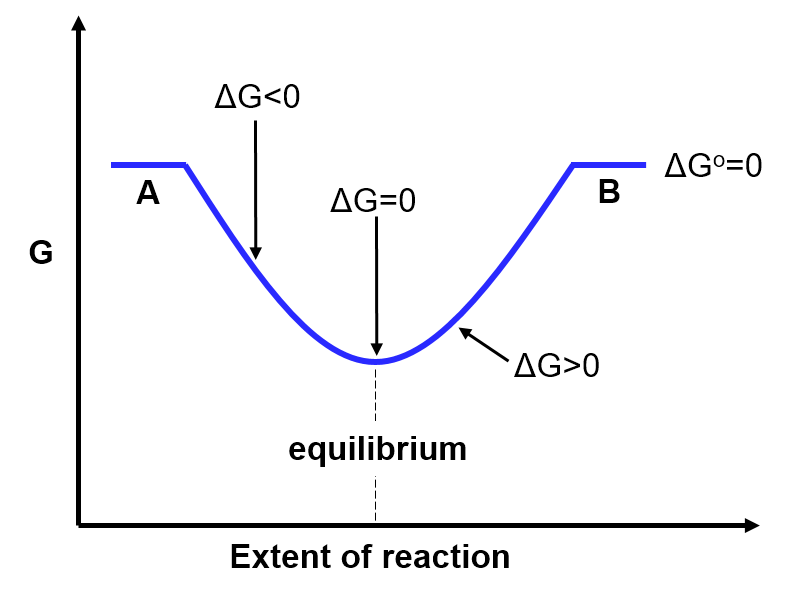
A and B have equal Gibbs free energy ( $\Delta G^{o}=0$ )
In the situation where A and B have the same Gibbs free energy ( $G_{A}^{o}=G_{B}^{o}$ ), we'd expect them to be present in equal amounts at equilibrium. Mathematically, if $\Delta G^{o}=0$ , then by equation 3

$\0=-RTlnK$

and thus $K=1$ . Since $K=\frac{[B]}{[A]}=1$ , this value of K means that there are an equal number of products and reactants at equilibrium ( $[A]=[B]$ ), as predicted.

This is illustrated in the graph below: The y-axis is the Gibbs free energy. The x-axis is the extent of the reaction (from 100% reactants / 0% products (left side) → 75% reactants / 25% products → 50% reactants / 50% products → 25% reactants / 75% products → 0% reactants / 100% products (right side)). The fact that $\Delta&space;G^{o}=0$ is reflected by the pure reactants (A) and pure products (B) being at the same height. The slope of the connecting blue line reflects the sign and magnitude of $\Delta&space;G$ . When mostly reactants are present (left side), the slope is negative and thus $\Delta&space;G<0$ and this reaction is spontaneous (i.e. it is thermodynamically favourable for the reaction to proceed forward towards equilibrium). When mostly products are present (right side), the slope of the line is positive and thus $\Delta&space;G>0$ and this reaction is non-spontaneous. Starting from mostly products, this reaction would proceed in the reverse direction towards equilibrium. The x-value when G is at its minimum value corresponds to the equilibrium position. At this point, the slope of the line is 0 and thus $\Delta&space;G=0$ . Notice that in this case where $G_{A}^{o}=G_{B}^{o}$ , the equilibrium position is exactly halfway between pure A and pure B. That is, this diagram illustrates that at equilibrium there are 50% products and 50% reactants, as described above.
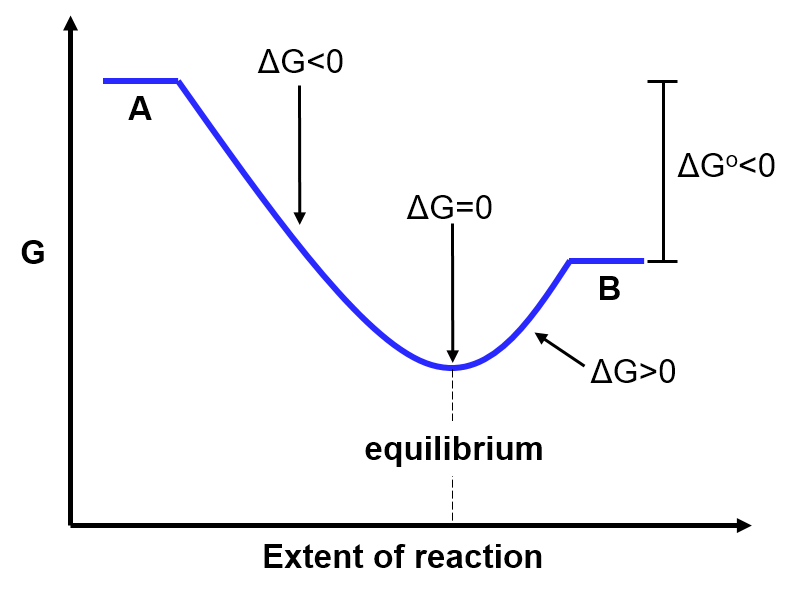
A has higher Gibbs free energy than B ( $\Delta G^{o}<0$ )
If the Gibbs free energy of A is higher than that of B ( $G_{A}^{o}>G_{B}^{o}$ ), then we'd expect there to be relatively more B than A at equilibrium. Mathematically, if $G_{A}^{o}$ is larger than $G_{B}^{o}$ , then $\Delta&space;G^{o}<0.$ Based on Equation 3 this means that $-RTlnK<0$ and thus K must be larger than 1 ( $K>1.$ ). When $K>1$ , the products are favoured at equilibrium, as predicted.

This is illustrated in the diagram below: notice that equilibrium (the lowest point on the graph when $\Delta&space;G=0$ ) occurs at a point along the x-axis that is closer to the pure products (B) than the pure reactants (A). This indicates that there are more products than reactants at equilibrium. This is the same situation that was depicted in the slider above.
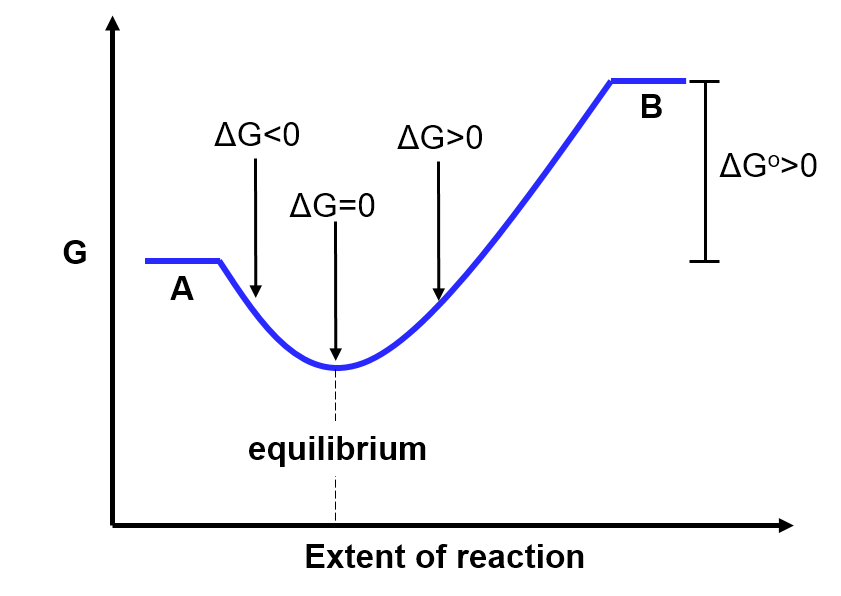
A has lower Gibbs free energy than B ( $\Delta G^{o}>0$ )
In the situation where the Gibbs free energy of A is lower than that of B ( $G_{A}^{o}<G_{B}^{o}$ ), we would predict that the equilibrium position would thus lie closer to the reactants (A). Mathematically, if $\Delta G^{o}=-RTlnK>0$ then $K<1$ . Since $K=\frac{[B]}{[A]}$ , this means that there are more reactants than products at equilibrium ( $[A]>[B]$ ) which matches our prediction.

This is also illustrated in the diagram below. The equilibrium position occurs at a point along the x-axis that is closer to the reactants (A) than the products (B). This indicates that there are more reactants than products at equilibrium.

+ Practice

Interactive:

+ Feedback

4.2: Standard Gibbs free energy

Search

Report