1.5: Second order integrated rate law

For the elementary reaction $2A\rightarrow B$ with $rate=-\frac{1}{2}\frac{d[A]}{dt}=k_{1}[A]^{2}$ , a plot of $\frac{1}{[A]}$ versus $t$ gives a straight line with slope $m=2k_1$ and y-intercept $b=\frac{1}{[A]_0}$ .

In this section we'll repeat the same procedure as in Section 1.4 to determine the relationship between concentration and time for a second order process. Please review the derivation in Section 1.4 first, especially if you are not familiar with integral calculus.

Consider the elementary reaction

$2A\rightarrow B$ .

The rate law for this reaction is

$rate=-\frac{1}{2}\frac{d[A]}{dt}=k_{1}[A]^{2}$ (Equation 1),

which means that this reaction is 2nd order with respect to A. Let's integrate this rate law to find the relationship between [A] and t for a second order process. First, rearrange Equation 1 to isolate the concentration terms on the left and the time terms on the right:

$\frac{1}{[A]^2}d[A]=-2k_{1}dt$ .

Next, integrate the left side from $[A]_{0}$ to $[A]_{t}$ and the right side from $t=0$ to time $t$ :

$\int_{[A]_{0}}^{[A]_{t}}\frac{1}{[A]^2}d[A]=\int_{0}^{t}-2kdt$

$-\frac{1}{[A]}\biggr\rvert_{[A]_{0}}^{[A]_{t}}=-2k_{1}t\biggr\rvert_{0}^{t}$

$-\frac{1}{[A]_{t}}+\frac{1}{[A]_0}=-2k_{1}t$ (Equation 2).

Integration help: What does this mean?

The integral of $\frac{1}{[A]^2}$ is $-\frac{1}{[A]}$ . You are not expected to know why this is true, but should be able to reproduce this result. You will not be asked to assess any unfamiliar integrals on CHEM 123 exams.

Rearranging Equation 2 to its linear form gives

$\frac{1}{[A]_t}=2k_{1}t+\frac{1}{[A]_0}$ ,

or, simply,

$\frac{1}{[A]}=2k_{1}t+\frac{1}{[A]_0}$ .

By analogy with the generic linear equation $y=mx+b$ , this means that a plot of $y=\frac{1}{[A]}$ vs $x=t$ gives a straight line with slope $m=2k_{1}$ and y-intercept $b=\frac{1}{[A]_{0}}$ .

Example: What is the rate constant for a second order process with the best fit line shown below?

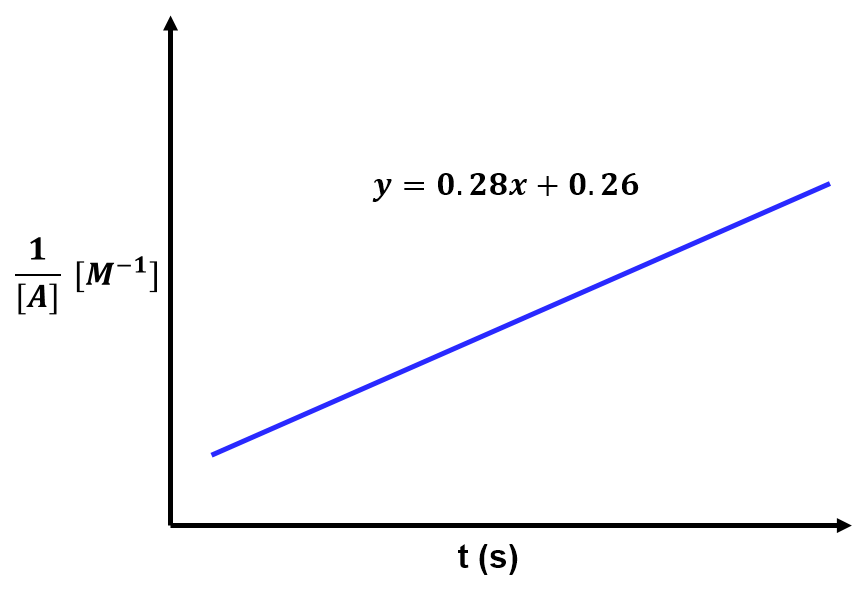
View solution:

The slope of the line relates to the rate constant by $m=2k$ . Based on the given best fit line,

$m=0.28Ms^{-1}M^{-1}$

and thus the rate constant is

$k=0.14s^{-1}M^{-1}$

In class / high school / a textbook I saw $\frac{1}{[A]}=k_{2}t+\frac{1}{[A]_0}$ . Why is the solution here different?

At the beginning of this section, we took the rate to be

$rate=\frac{d[B]}{dt}=-\frac{1}{2}\frac{d[A]}{dt}=k_{1}[A]^{2}$ (Equation 1).

The '2' in this rate law carried forward to give the 2 in our final solution

$\frac{1}{[A]}=2k_{1}t+\frac{1}{[A]_0}$ .

Some chemists prefer to set the overall reaction rate relative to one mole of reactants (instead of one mole of the products as we did above) such that the rate is

$rate=-\frac{d[A]}{dt}=2\frac{d[B]}{dt}=k_{2}[A]^{2}$ .

Note that we have called the rate constant $k_{2}$ here instead of $k_{1}$ , since defining the rate differently also gives us a different rate constant. There is nothing fundamentally different about this approach. Starting from this rate law, we proceed through the same steps to give
$\frac{1}{[A]^2}d[A]=-k_{2}dt$ .

$\int_{[A]_{0}}^{[A]_{t}}\frac{1}{[A]^2}d[A]=\int_{0}^{t}-k_{2}dt$

$-\frac{1}{[A]}\biggr\rvert_{[A]_{0}}^{[A]_{t}}=-k_{2}t\biggr\rvert_{0}^{t}$

$-\frac{1}{[A]_{t}}+\frac{1}{[A]_0}=-k_{2}t$

and finally
$\frac{1}{[A]}=k_{2}t+\frac{1}{[A]_0}$ .

Note that by analogy, it must be that $k_{2}=2k_{1}$ .