2.2: Eyring equation

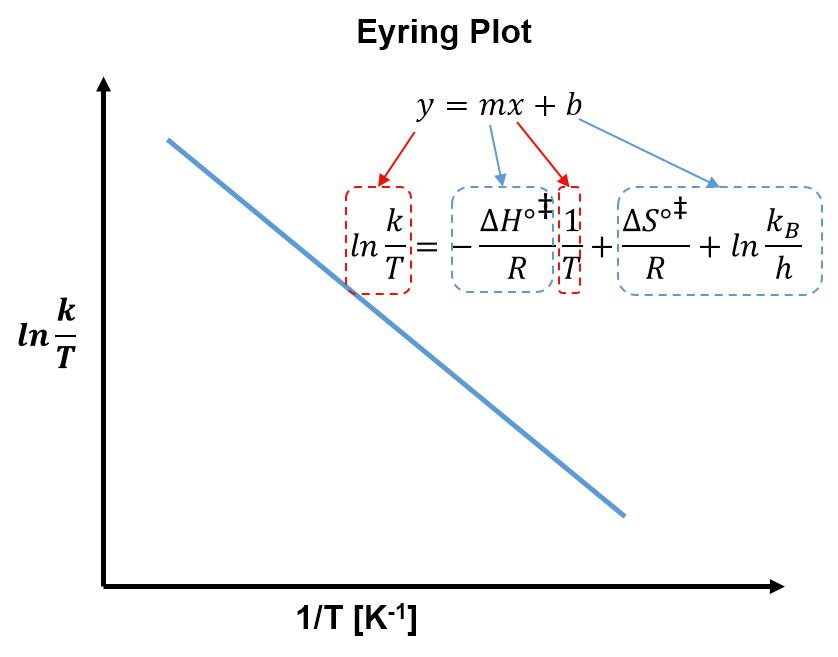
The linear form of the Eyring equation is $ln\frac{k}{T}=-\frac{\Delta H^{o\ddagger}}{RT}+\frac{\Delta S^{o\ddagger}}{R}+ln\frac{k_B}{h}$
A plot of $ln{\frac{k}{T}}$ versus $\frac{1}{T}$ gives a straight line with slope $m=-\frac{\Delta H^{o\ddagger}}{R}$ and y-intercept $b=\frac{\Delta S^{o\ddagger}}{R}+ln\frac{k_B}{h}$ .

While useful and still widely used, the Arrhenius equation,

$k=Ae^{-\frac{E_A}{RT}}$ (Equation 1),

is somewhat unsatisfying in that it relies on an experimentally determined proportionality constant, A, for each reaction. The Eyring equation (Equation 2),

$k=\frac{k_{B}T}{h}e^{-\frac{\Delta G^{\ddagger}}{RT}}$ (Equation 2),

is an analogous equation for the free energy of activation, $\Delta&space;G$ ^‡, instead of the activation energy, and eliminates the need for this reaction-specific proportionality constant. In Equation 2, R is the universal gas constant ( $8.314 \frac{J}{molK}$ ), T is the temperature (in Kelvin), h is the Planck constant ( $6.626 \times 10^{-34} Js$ ), and k_B is the Boltzmann constant ( $1.38\times 10^{-23} \frac{J}{K}$ ). The derivation of the Eyring equation will not be examined in CHEM 123, but is included below for your interest.

Derivation: Expand this section to see the derivation of Equation 2.

Video derivation:

Text-based derviation:
We can derive most of Equation 2 with concepts from CHEM 123, though, as you'll see below, the details of one step in the derivation will only come in later chemistry courses.

Imagine the reaction

$A+B\rightarrow C$

with the reaction coordinate diagram:

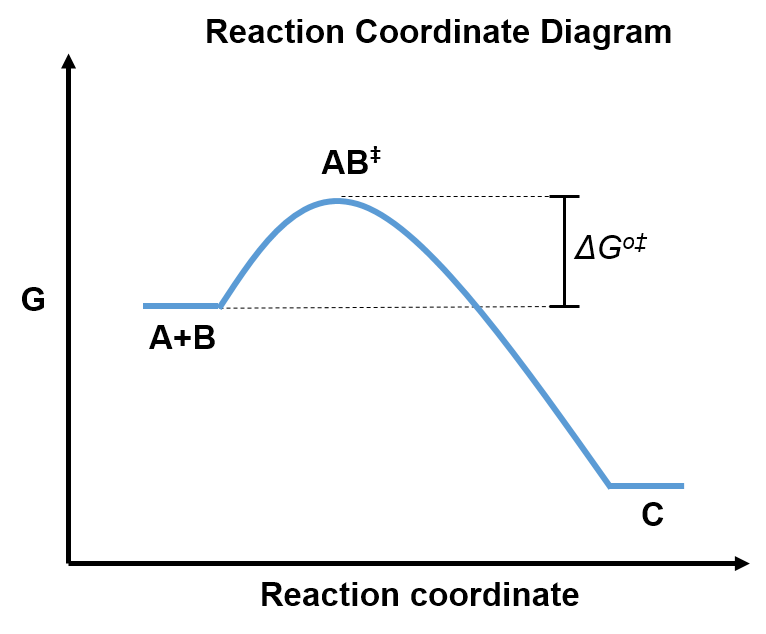
eyring reaction coord

We can consider this reaction in two stages: first, the reactants (A and B) form the transition state ( $AB^\ddagger$ ), then the transition state transforms into the product (C), such that

$A+B\overset{K^\ddagger}\leftrightharpoons AB^\ddagger \overset{k^\ddagger}\rightarrow C$

where $k^\ddagger$ is the rate constant that describes the how quickly the transition state transforms into the product, and $K^\ddagger$ is the equilibrium constant between the the reactants and transition state given by

$K^\ddagger=\frac{[AB]^\ddagger}{[A][B]}$ (Equation 3).

Considering the second stage of this process,

$[AB]^\ddagger\overset{k^\ddagger}\rightarrow C$ ,

the products are formed at the rate that the transition state transforms into product such that

$rate=k^\ddagger[AB]^\ddagger$ .

Solving Equation 3 for $[AB]^\ddagger$ gives

$[AB]^\ddagger=K^{\ddagger}[A][B]$

and thus the rate is

$rate=k^{\ddagger}K^{\ddagger}[A][B]$ (Equation 4).

Since $A+B\overset{k}\rightarrow C$ is an elementary reaction, we could also describe the rate as

$rate=k[A][B]$ (Equation 5).

By comparison of Equations 4 and 5, it must be that

$k=k^{\ddagger}K^{\ddagger}$ (Equation 6).

Now consider the first stage of this reaction:

$A+B\overset{K^{\ddagger}}\leftrightharpoons [AB]^{\ddagger}$ .

Since the standard Gibbs free energy difference relates to the equilibrium constant (see Part 1 Section 4.2), here the free energy of activation, $\Delta G^{o\ddagger}$ , relates to the equilibrium constant, $K^{\ddagger}$ , between the reactants and transition state by

$\Delta G^{o\ddagger}=-RTlnK^{\ddagger}$

such that

$K^{\ddagger}=e^{-\frac{\Delta G^{o\ddagger}}{RT}}$ .

Equation 6 thus can also be written as

$k=k^{\ddagger}e^{-\frac{\Delta G^{o\ddagger}}{RT}}$ (Equation 7).

Finally, the rate constant, $k^{\ddagger}$ , for the the transformation of the transition state to products is given by

$k^{\ddagger}=\frac{k_BT}{h}$ .

The details of this step are beyond the scope of CHEM 123. Substituting this new term for $k^{\ddagger}$ into Equation 7 gives the Eyring equation

$k=\frac{k_BT}{h}e^{-\frac{\Delta G^{o\ddagger}}{RT}}$ (Equation 2).

The standard free energy of activation relates to the standard enthalpy of activation, $\Delta H^{o\ddagger}$ , and the standard entropy of activation, $\Delta S^{o\ddagger}$ , by

$\Delta G^{o\ddagger}=\Delta H^{o\ddagger}-T\Delta S^{o\ddagger}$ .

Thus, the Eyring equation (Equation 2) can also be written as

$k=\frac{k_BT}{h}e^{-\frac{\Delta H^{o\ddagger}-T\Delta S^{o\ddagger}}{RT}}=\frac{k_BT}{h}e^{-\frac{\Delta H^{o\ddagger}}{RT}}e^{\frac{\Delta S^{o\ddagger}}{R}}$ (Equation 8).

Dividing both sides of Equation 8 by T gives

$\frac{k}{T}=\frac{k_B}{h}e^{-\frac{\Delta H^{o\ddagger}}{RT}}e^{\frac{\Delta S^{o\ddagger}}{R}}$

and taking the natural logarithm of both sides and rearranging gives

$ln\frac{k}{T}=-\frac{\Delta H^{o\ddagger}}{RT}+\frac{\Delta S^{o\ddagger}}{R}+ln\frac{k_B}{h}$ (Equation 9).

Equation 9 is a useful form of the Eyring equation because a plot of $y=ln\frac{k}{T}$ versus $x=\frac{1}{T}$ gives a linear plot with slope

$m=-\frac{\Delta H^{o\ddagger}}{R}$

and y-intercept

$b=\frac{\Delta S^{o\ddagger}}{R}+ln\frac{k_B}{h}$ .

That is, Equation 9 can be used to calculate $\Delta H^{o\ddagger}$ and $\Delta S^{o\ddagger}$ (and thus also $\Delta G^{o\ddagger}$ ) when given temperature and rate constant data.

+ Practice

Interactive:

+ Feedback

Last updated on February 14, 2019 @11:46 am

2.2: Eyring equation

Search

Report